Что такое возведение в степень, как возводить в степень действительное число. Как связаны степень и умножение.
Степень действительного числа a с натуральным показателем n есть произведение n сомножителей, каждый из которых равен а:
a^1=a, \\ a^2=a \cdot a, \\ a^n= \underbrace{a \cdot a \cdot a ... a}_{n раз},Например,
\displaystyle 2^5=\underbrace{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}_{5}=32\\ \\ \displaystyle (-3)^4= \underbrace {(-3) \cdot (-3) \cdot (-3) \cdot (-3)}_{4}=81\\ {}.
Действительное число a называется основанием степени, а натуральное число n — показателем степени.
Правила возведения в степень
Справедливы следующие правила:
- Чтобы возвести в степень произведение, нужно возвести в эту степень каждый сомножитель отдельно, а результаты перемножить: (abc)^n=a^{n}b^{n} c^{n} \\ {}.
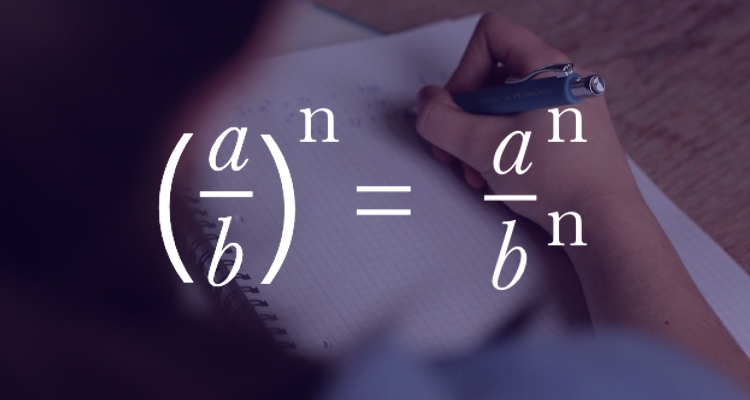
Возведение в степень дроби - Чтобы возвести в степень дробь, нужно возвести в эту степень числитель и знаменатель отдельно и первый результат разделить на второй: \displaystyle (\frac{a}{b})^n=\frac{a^n}{b^n} \\ {}.
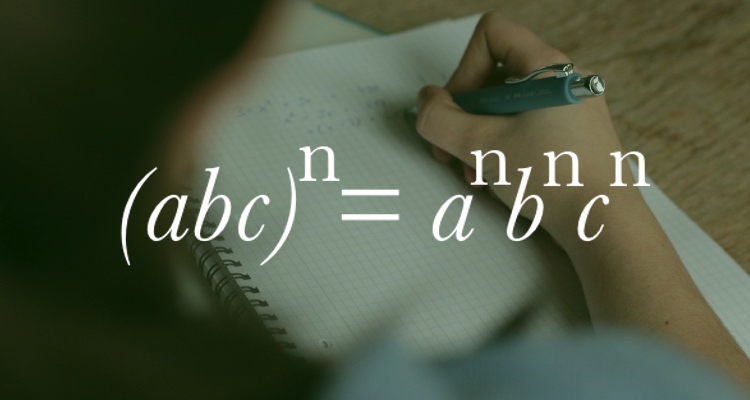
Возведение в степень произведения
Свойства степеней
Имеют место следующие свойства степеней, которые мы в дальнейшем будем называть правилом знаков.
- Любая степень положительного числа есть число положительное. Например, 2^4=16, \\ 5^3=125, \\ \displaystyle (\frac{1}{3})^3=\frac{1}{27}, \\ (0,1)^5=0,00001.
- Четная степень отрицательного числа есть число положительное. Так, \displaystyle (-2)^2=(-2)(-2)=4; \\ \displaystyle (-\frac{1}{3})^4=(-\frac{1}{3})(-\frac{1}{3})(-\frac{1}{3})(-\frac{1}{3})=\frac{1}{81}.
- Нечетная степень отрицательного числа есть число отрицательное. Приведем пример: \displaystyle (-3)^3=(-3)(-3)(-3)=-27, \\ \displaystyle (-\frac{1}{2})^5=(-\frac{1}{2})(-\frac{1}{2})(-\frac{1}{2})(-\frac{1}{2})(-\frac{1}{2})=-\frac{1}{32}


хорошая статья.поучительная.спасибо.
Вау уже всё позабывал.
Вспомнил студенческие годы.
Школьная программа 7 класс.
Поверите, или нет, но вот ни разу мне это не пригодилось за 30 лет после школы.
Я уже все формулы и забыла, сколько всего дети изучают.
Хороший урок, в математике поможет!)
для меня трудная тема. я и раньше когда учился в этом был не силен.
У меня с алгеброй в школе были проблемы но все равно статья понравилась
Помню когда в школе эти степени проходили, я тогда нечего не понимал в них как бы мне не объясняли. Я сейчас сижу читаю эту статью, и понимаю, что вроде нечего сложного тут нету
Очень подробно и понятно всё объяснено,благодарю.